说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

题目描述

小姬最近开始研究起了曼哈顿距离，因为他厌倦了欧氏距离的学习。

我们知道，平面内 (x1,y1) 与 (x2,y2) 的曼哈顿距离被定义为这两点在标准坐标系上的绝对轴距之和，即 |x1−x2|+|y1−y2|。

对于小姬来讲，他可以很容易的算出给定平面内任意多个点之间的曼哈顿距离，但是千千给小姬出了一个问题：假如我有 n(n−1)2 个数，它们分别代表平面中 n
个点之间的曼哈顿距离，你能告诉我这 n 个点的位置么？

随后的几天，小姬开始困惑了，因为他想来想去也只会算当 n=2 的情形，于是便去找千千诉苦，看到这样的情形，千千只好答应降低难度，只要你算出 n=3
的情形便可以啦。

你能帮小姬解决这个问题么？

输入

输入只有一行，包含三个正整数 a,b,c (1≤a,b,c≤100)，分别代表平面中 3 个点两两之间的曼哈顿距离。（保证输入数据有解）

输出

输出满足题意的三个点的坐标（要求
0≤|x|,|y|≤105），每个点的坐标占一行，可以以任意的顺序输出，若存在多解的情况，输出任意一组即可。（如果你的答案计算出的结果与真实值相差 10−6
以内则被认为是正确的）

样例输入

1 1 2

样例输出

0.000000 0.000000
1.000000 0.000000
0.000000 1.000000

思路

在这三个曼哈顿距离中任取一个d，它一定表示两点之间的曼哈顿距离
设其中一个点为原点，则另一个点一定在以原点为中心距离远点曼哈顿距离为d的菱形（正方形）上。
其他两个输入值，其中有一个值是于原点相关的曼哈顿距离，而这个值对应的点也应该是围绕原点的一个菱形（正方形）
。
不妨先假设其中一个值是与原点相关的曼哈顿距离，只要第三个值（原点除外的其他两点的曼哈顿距离）在区间【两菱形之间点的最短距离，两菱形点的最长距离】范围之内，则必定可以求解，如果不满足，则最后剩下的值才是与原点关联的值
。
这样我们就可以先直接定死两个点，求第三个点。
先说两个菱形大小不一样的情况：
如下图，（这个图我只看了右边）
1.我定的点是（0，0）和小菱形最上端的点（0，x）
图中上方表示红线（0，x）和求解点有最短距离时求解点存在的范围，在这一线段上（0，x）和求解点的曼哈顿距离相等，这个最短距离为abs（与原点相关的连个曼哈顿距离只差），若不关联原点的曼哈顿距离就是最短距离，则随便取红线上的一点就是答案
2.同理，下方红线表示（0，x）和所求点曼哈顿距离最长的范围，若不关联原点的曼哈顿距离等于最长距离，则随便在下方红线上取一点就是答案
3.在蓝线上（0，x）到求解点的曼哈顿距离递增
我们可以先把求解点定在上方红线的最下边，这时求解点与（0，x）的曼哈顿距离为最短距离，然后再将求解点向下偏移，令两点之间的曼哈顿距离增长（不关联原点的曼哈顿距离-
最短距离），得到的点就是答案（斜率都是1或-1呀）
![在这里插入图片描述](https://img-blog.csdnimg.cn/20201028223150512.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dsZGNtenk=,size_16,color_FFFFFF,t_70#pic_center)
如果两个菱形大小一样，最上方的红线就会变成一个点，其余思路不变，所以这种情况不用另外考虑 战吼：放一个P

代码

一遍过的，里面有些冗余的东西写出来了根本没用上，比如那个结构体的点

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>

struct Edge
{
    float x,y;
}p1,p2,p3;
int a,b,c;

void fun(float p,float q,float w)
{
    float x,y,px,py,left;
    if(p<q) x=p,y=q;
    else x=q,y=p;
    if (w == std::abs(p-q))
    {
        px=0;
        py=y;
    }
    else if(w == p+q)
    {
        px=0;
        py=-y;
    }
    else
    {
        float tmp=std::abs(p-q);
        px=tmp,py=x;
        left=w-tmp;
        left/=2;
        px+=left;
        py-=left;
    }
    printf("%.6f %.6f\n",0.0,0.0);
    printf("%.6f %.6f\n",0.0,x);
    printf("%.6f %.6f\n",px,py);

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

}

int main()
{
    std::cin >> a >> b >> c;
    p1.x=p1.y=0;
    if(c>= std::abs(a-b) && c<= a+b)
    {
        fun(a,b,c);
    }
    else
    {
        fun(a,c,b);
    }

    return 0;
}

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

指定仓库的用户名和邮箱，–global表示这台机器的所有仓库都用这个用户名或邮箱

wldcmzy@DESKTOP-UL0SE7R MINGW64 /D/test (master)
$ git config --global user.name “wldcmzy”
wldcmzy@DESKTOP-UL0SE7R MINGW64 /D/test (master)
$ git config --global user.email “wldcmzy@163.com”

将一个目录变为git可以管理的仓库

cd 一个目录
git init

git add：将文件提交到暂存区
git commit -m：将暂存区文件提交到仓库（单引号内为注释）

git status：检查当前文件状态 git diff：查看文件修改的内容

git log：获得历史修改记录
git log --pretty=oneline：使记录只显示主要的内容，一行显示

git reflog：获取历史版本号
git reset --hard 版本号：回退到该版本号对应的版本
git reset --hard HEAD^：回退到上1个版本
git reset --hard HEAD^^：回退到上2个版本
git reset --hard HEAD~50：回退到上50个版本

好像是创造一个readme文件，否则以后push会出错

git pull --rebase origin master

git remote add origin https://github.com/Wldcmzy/test.git 关联仓库

git push origin master 推送到仓库

git checkout -b xxx

git checkout xxx

参考资料
https://www.cnblogs.com/imyalost/p/8777684.html
https://www.cnblogs.com/imyalost/p/8762522.html

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

抄了半个大致模板 自己研究了研究了研究，现在先会画流程图 改日详细填坑

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

from graphviz import Digraph
from graphviz import Source
dot = Digraph(
    name='try1',
    comment='',
    filename=None,
    directory=None,
    format="png",
    engine=None,
    encoding='utf8',
    graph_attr={'rankdir':'TB'},
    node_attr={'color':'black','fontcolor':'black','fontname':'FangSong','fontsize':'12','style':'rounded','shape':'box'},
    edge_attr={'color':'red','fontcolor':'#888888','fontsize':'10','fontname':'FangSong'},
    body=None,
    strict=False
)
dot.node('A','A-----',shape = 'rectangle')
dot.node('B','B=====',shape = 'circle')
dot.node('C', 'C-----',shape = 'triangle', color = 'blue', fontcolor = 'green')
dot.node('D','D=====',shape = 'circle')
dot.view()
'try1.gv.png'
dot.edge('A','B','E GAY WOLY GIAO')
dot.edge('A','D','ss')
dot.edge('D','C')
dot.edge('C','A')
dot.edge('C','D')
dot.view()
'try1.gv.png'

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

2021/04/21：我火星了？？？？

python Seaborn库 调色板

所以下面的东西都别看了

.

.

.

.

.

.

.

.

.

.

由来

昨天画了这张图，自动分配的颜色比较深，而且总颜色数不多，这张图的颜色是自己一点一点写的，很麻烦，所以想制作一个简单的颜色序列生成器一劳永逸
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210209193159338.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dsZGNtenk=,size_16,color_FFFFFF,t_70#pic_center)

介绍

我给这个文件取名为InterestingColorfulColor.py，把它放在python安装目录的Lib文件夹就可以随时用import语句导入，非常方便。
例如：

​

1

import InterestingColorfulColor as ICC

目前这个文件的主要内容只有一个类：ColorOrder
ColorOrder类里给出了15种按照颜色深浅梯度变化的基础颜色序列，分别为：
红，红橙，橙，橙黄，黄，黄绿，绿，绿青，青，青蓝，蓝，蓝紫，紫，紫红，和灰色 （由纯黑到纯白）
每种序列有16种不同的颜色。
通过这个类可以较为轻松地得到一种你想要的颜色序列 ，有可能可以让你的工作提高一点点效率。不过这毕竟是个小制作，功能不复杂。
下图展示其中一部分颜色
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210209193935836.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dsZGNtenk=,size_16,color_FFFFFF,t_70#pic_center)

使用

约定

约定上述15种颜色序列为 gray red, orange,yellow,green,cyan,blue,purple
以及除了gray外剩下七种颜色中相邻颜色之间的两两组合 如redorange,
greencyan等，对两种颜色书写的先后顺序不做要求即redpurple和purplered都是正确的

导入模块

​

1

import InterestingColorfulColor as ICC

创建一个ColorOrder对象

​

1

co = ICC.ColorOrder(['red','blue'],mixtype = 'cross')

参数解析：
def init (self, colornames, mixtype = ‘Connect’)
两个参数，colornames ， mixtype

参数colornamse给出若干个颜色序列的名称。
参数mixtype表示混合这些颜色序列的方式，目前只有两个值：connect 和 cross （不需要区分大小写）
connect为默认值 以连接的方式混合，即按照顺序依次把colornames中给出的颜色序列首尾相接
cross 以交叉的方式混合 。举个例子 如果以cross的方式混合三个颜色序列[1,2,3][a,b,c][x,y,z]
最后的结果序列为[1,a,x,2,b,y,3,c,z]

查看颜色序列，以及其他两个隐藏属性

​

1
2
3
4
5
6
7
8

co.getOrder() #查看序列
co.getLength() #查看序列长度
co.getBaseOrderNumber() #查看该序列由几个基础序列混合而成

结果：
['#2F0000', '#000079', '#4D0000', '#000093', '#600000', '#0000C6', '#750000', '#0000C6', '#930000', '#0000E3', '#AE0000', '#2828FF', '#CE0000', '#4A4AFF', '#EA0000', '#6A6AFF', '#FF0000', '#7D7DFF', '#FF2D2D', '#9393FF', '#FF5151', '#AAAAFF', '#ff7575', '#B9B9FF', '#FF9797', '#CECEFF', '#FFB5B5', '#DDDDFF', '#FFD2D2', '#ECECFF', '#FFECEC','#FBFBFF']
32
2

切片获取序列

​

1
2
3

co.getLeft(False) #获得序列左边的25%
co.getRight(True) #获得序列右边的25%
co.getMiddle() #获得序列中间的50%

参数分析：
def getLeft(self, muti_section = False):
三个方法只有一个相同的参数，muti_section
当muti_section默认为False 直接根据需求获得序列的前25%或后25%或中间50%
当muti_section为True， 考虑某些时候切片以connect方式混合的序列，他会单独提取每个基础序列的左、右或中间的部分，拼接到一起作为返回结果

与ColorOrder对象的序列混合

​

1

co.mix(co,'cross')

参数解析：
def mix(self, co, mixtype = ‘Connect’)
co为实例对象，mixtype与__init__中的mixtype相同
值得一提的是这时两个序列不一定时等长的，我们再举一个cross混合的例子。假设混合[2,3,4,2,3,4,2,3,4]和[0,1,0,1,0,1]两个序列，最后的结果是[2,3,4,0,1,2,3,4,0,1,2,3,4,0
1]

应用简例

​

1
2
3
4
5
6
7
8
9
10
11

%matplotlib inline
import InterestingColorfulColor as ICC
import matplotlib.pyplot as plt

fig, ax = plt.subplots(1,2,figsize = (16,8))

co = ICC.ColorOrder(['blue','redpurple'],'cross')
ax[0].pie([1]*len(co.getOrder()),colors = co.getOrder())

co.mix(ICC.ColorOrder(['Green']),'cross')
ax[1].pie([1]*len(co.getMiddle()),colors = co.getMiddle())

效果：
![在这里插入图片描述](https://img-blog.csdnimg.cn/20210209204037167.png?x-oss-
process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dsZGNtenk=,size_16,color_FFFFFF,t_70#pic_center)

%……&%￥……？？？？？！！！

弄到颜色序列之后是可以用co.getOrder()导出来自己随便切的，并不是只能按照getMiddle,getLeft,getRight的固定方式切片

源代码

​

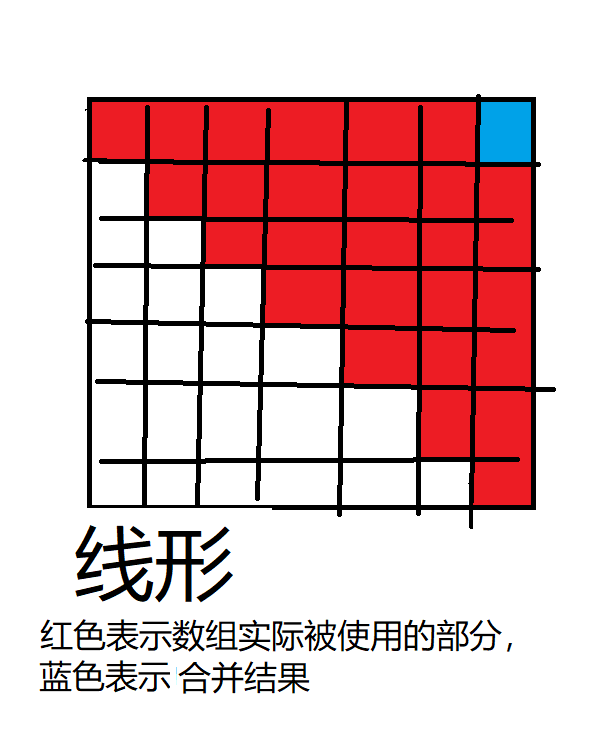
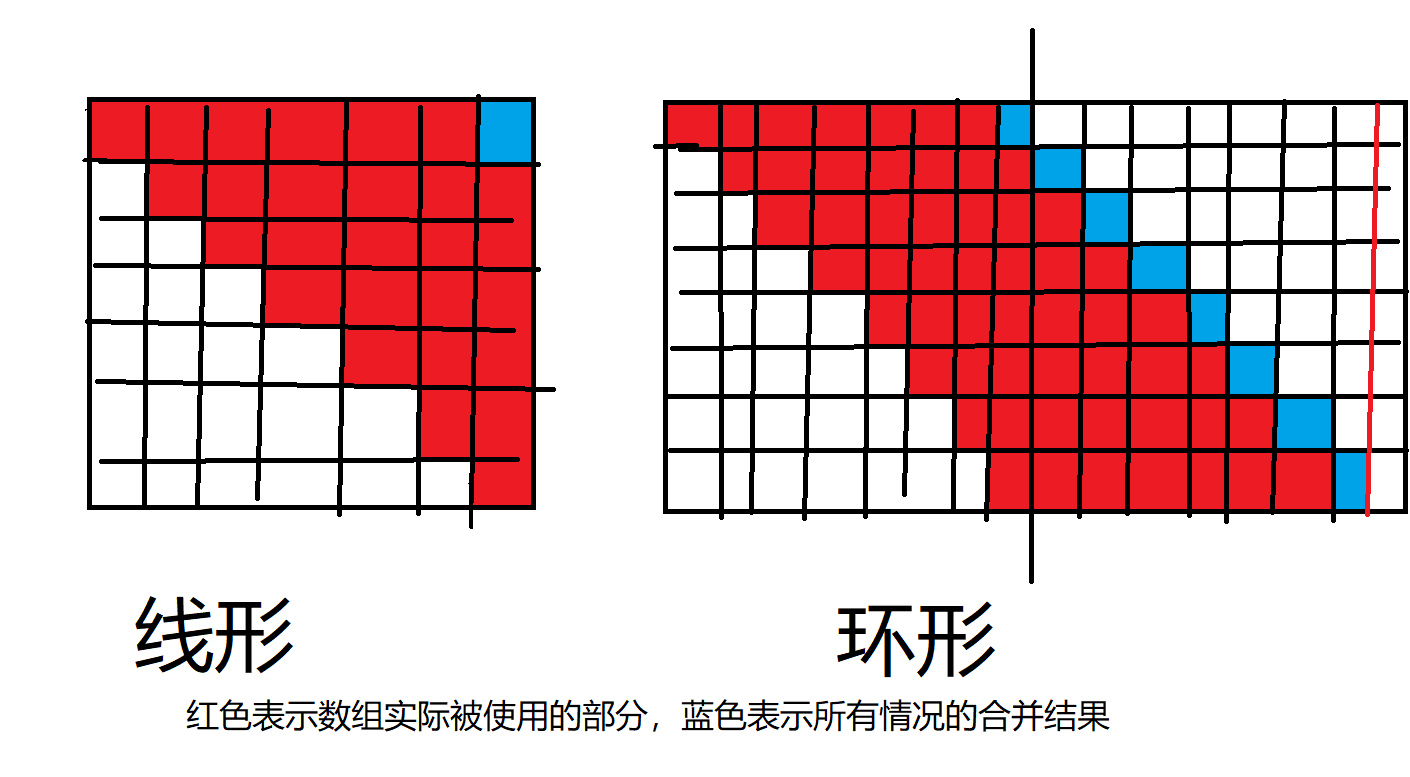
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143

class ICC_UnknowColorName(Exception):
    pass
class ICC_UnknowMixType(Exception):
    pass

class ColorOrder:
    BaseOrderLength_Normal = 16
    #BaseOrderLength_Dull   = 12
    ErrorText_ICC_UnknowColorName = 'Exist color name not in ColorOrder.ColorMap, can not identify what color the name means. Or you need to use an iteratable object to iteratable object all color names'
    ErrorText_ICC_UnknowMixType = 'Can not identify mixtype'
    ColorMap = { 
         'Gray'        : 'Gray'
        ,'Red'         : 'Red'
        ,'Redpurple'   : 'RedPurple'
        ,'Purplered'   : 'RedPurple'
        ,'Purple'      : 'Purple'
        ,'Purpleblue'  : 'PurpleBlue'
        ,'Bluepurple'  : 'PurpleBlue'
        ,'Blue'        : 'Blue'
        ,'Bluecyan'    : 'BlueCyan'
        ,'Cyanblue'    : 'BlueCyan'
        ,'Cyan'        : 'Cyan'
        ,'Cyangreen'   : 'CyanGreen'
        ,'Greencyan'   : 'CyanGreen'
        ,'Green'       : 'Green'
        ,'Greenyellow' : 'GreenYellow'
        ,'Yellowgreen' : 'GreenYellow'
        ,'Yellow'      : 'Yellow'
        ,'Yelloworange': 'YellowOrange'
        ,'Orangeyellow': 'YellowOrange'
        ,'Orange'      : 'Orange'
        ,'Orangered'   : 'OrangeRed'
        ,'Redorange'   : 'OrangeRed'
        #,'Dullred'     : 'DullRed'
        #,'Dullyellow'  : 'DullYellow'
        #,'Dullcyan'    : 'DullCyan'
        #,'Dullblue'    : 'DullBlue'
        #,'Dullpurple'  : 'DullPurple'
    }
    BaseColorOrder = { 
         'Gray'        :   ['#ffffff','#272727','#3C3C3C','#4F4F4F','#5B5B5B','#6C6C6C','#7B7B7B','#8E8E8E','#9D9D9D','#ADADAD','#BEBEBE','#d0d0d0','#E0E0E0','#F0F0F0','#FCFCFC','#FFFFFF']
        ,'Red'         :   ['#2F0000','#4D0000','#600000','#750000','#930000','#AE0000','#CE0000','#EA0000','#FF0000','#FF2D2D','#FF5151','#ff7575','#FF9797','#FFB5B5','#FFD2D2','#FFECEC']
        ,'RedPurple'   :   ['#600030','#820041','#9F0050','#BF0060','#D9006C','#F00078','#FF0080','#FF359A','#FF60AF','#FF79BC','#FF95CA','#ffaad5','#FFC1E0','#FFD9EC','#FFECF5','#FFF7FB']
        ,'Purple'      :   ['#460046','#5E005E','#750075','#930093','#AE00AE','#D200D2','#E800E8','#FF00FF','#FF44FF','#FF77FF','#FF8EFF','#ffa6ff','#FFBFFF','#FFD0FF','#FFE6FF','#FFF7FF']
        ,'PurpleBlue'  :   ['#28004D','#3A006F','#4B0091','#5B00AE','#6F00D2','#8600FF','#921AFF','#9F35FF','#B15BFF','#BE77FF','#CA8EFF','#d3a4ff','#DCB5FF','#E6CAFF','#F1E1FF','#FAF4FF']
        ,'Blue'        :   ['#000079','#000093','#0000C6','#0000C6','#0000E3','#2828FF','#4A4AFF','#6A6AFF','#7D7DFF','#9393FF','#AAAAFF','#B9B9FF','#CECEFF','#DDDDFF','#ECECFF','#FBFBFF']
        ,'BlueCyan'    :   ['#000079','#003D79','#004B97','#005AB5','#0066CC','#0072E3','#0080FF','#2894FF','#46A3FF','#66B3FF','#84C1FF','#97CBFF','#ACD6FF','#C4E1FF','#D2E9FF','#ECF5FF']
        ,'Cyan'        :   ['#003E3E','#005757','#007979','#009393','#00AEAE','#00CACA','#00E3E3','#00FFFF','#4DFFFF','#80FFFF','#A6FFFF','#BBFFFF','#CAFFFF','#D9FFFF','#ECFFFF','#FDFFFF']
        ,'CyanGreen'   :   ['#006030','#01814A','#019858','#01B468','#02C874','#02DF82','#02F78E','#1AFD9C','#4EFEB3','#7AFEC6','#96FED1','#ADFEDC','#C1FFE4','#D7FFEE','#E8FFF5','#FBFFFD']
        ,'Green'       :   ['#006000','#007500','#009100','#00A600','#00BB00','#00DB00','#00EC00','#28FF28','#53FF53','#79FF79','#93FF93','#A6FFA6','#BBFFBB','#CEFFCE','#DFFFDF','#F0FFF0']
        ,'GreenYellow' :   ['#467500','#548C00','#64A600','#73BF00','#82D900','#8CEA00','#9AFF02','#A8FF24','#B7FF4A','#C2FF68','#CCFF80','#D3FF93','#DEFFAC','#E8FFC4','#EFFFD7','#F5FFE8']
        ,'Yellow'      :   ['#424200','#5B5B00','#737300','#8C8C00','#A6A600','#C4C400','#E1E100','#F9F900','#FFFF37','#FFFF6F','#FFFF93','#FFFFAA','#FFFFB9','#FFFFCE','#FFFFDF','#FFFFF4']
        ,'YellowOrange':   ['#5B4B00','#796400','#977C00','#AE8F00','#C6A300','#D9B300','#EAC100','#FFD306','#FFDC35','#FFE153','#FFE66F','#FFED97','#FFF0AC','#FFF4C1','#FFF8D7','#FFFCEC']
        ,'Orange'      :   ['#844200','#9F5000','#BB5E00','#D26900','#EA7500','#FF8000','#FF9224','#FFA042','#FFAF60','#FFBB77','#FFC78E','#FFD1A4','#FFDCB9','#FFE4CA','#FFEEDD','#FFFAF4']
        ,'OrangeRed'   :   ['#642100','#842B00','#A23400','#BB3D00','#D94600','#F75000','#FF5809','#FF8040','#FF8F59','#FF9D6F','#FFAD86','#FFBD9D','#FFCBB3','#FFDAC8','#FFE6D9','#FFF3EE']
        #,'DullRed'     :   ['#613030','#743A3A','#804040','#984B4B','#AD5A5A','#B87070','#C48888','#CF9E9E','#D9B3B3','#E1C4C4','#EBD6D6','#F2E6E6']
        #,'DullYellow'  :   ['#616130','#707038','#808040','#949449','#A5A552','#AFAF61','#B9B973','#C2C287','#CDCD9A','#D6D6AD','#DEDEBE','#E8E8D0']
        #,'DullCyan'    :   ['#336666','#3D7878','#408080','#4F9D9D','#5CADAD','#6FB7B7','#81C0C0','#95CACA','#A3D1D1','#B3D9D9','#C4E1E1','#D1E9E9']
        #,'DullBlue'    :   ['#484891','#5151A2','#5A5AAD','#7373B9','#8080C0','#9999CC','#A6A6D2','#B8B8DC','#C7C7E2','#D8D8EB','#E6E6F2','#F3F3FA']
        #,'DullPurple'  :   ['#6C3365','#7E3D76','#8F4586','#9F4D95','#AE57A4','#B766AD','#C07AB8','#CA8EC2','#D2A2CC','#DAB1D5','#E2C2DE','#EBD3E8']
      }
    
    def __init__(self, colornames, mixtype = 'Connect'):
        colornames = [i.capitalize() for i in colornames]
        mixtype = mixtype.capitalize()
        for each in colornames:
            if each not in ColorOrder.ColorMap:
                raise ICC_UnknowColorName(ColorOrder.ErrorText_ICC_UnknowColorName)
                
        self.__order = []
        if mixtype == 'Connect':
            for eachname in colornames:
                self.__order.extend(ColorOrder.BaseColorOrder[ColorOrder.ColorMap[eachname]])
        elif mixtype == 'Cross':
            lst = []
            for eachname in colornames:
                lst.append(ColorOrder.BaseColorOrder[ColorOrder.ColorMap[eachname]])
            for i in range(ColorOrder.BaseOrderLength_Normal):
                for each in lst:
                    self.__order.append(each[i])
        else:
            raise ICC_UnknowMixType(ColorOrder.ErrorText_ICC_UnknowMixType)
            
        self.__baseOrderNumber = len(colornames)
        self.__length = self.__baseOrderNumber * ColorOrder.BaseOrderLength_Normal
    
    def getBaseOrderNumber(self):
        return self.__baseOrderNumber
    
    def getLength(self):
        return self.__length
    
    def getOrder(self):
        return self.__order.copy()
    
    def getLeft(self, muti_section = False):
        if muti_section == False:
            lst = self.__order[ : 4 * self.__baseOrderNumber ]
        else:
            lst = []
            for i in range(self.__baseOrderNumber):
                pos = i * ColorOrder.BaseOrderLength_Normal
                lst.extend(self.__order[ pos : pos + 4])
        return lst
    
    def getRight(self, muti_section = False):
        if muti_section == False:
            lst = self.__order[ -4 * self.__baseOrderNumber : ]
        else:
            lst = []
            for i in range(1,self.__baseOrderNumber+1):
                pos = i * ColorOrder.BaseOrderLength_Normal
                lst.extend(self.__order[ pos - 4 : pos])
        return lst
    
    def getMiddle(self, muti_section = False):
        if muti_section == False:
            lst = self.__order[ 4 * self.__baseOrderNumber : 12 * self.__baseOrderNumber ]
        else:
            lst = []
            for i in range(self.__baseOrderNumber):
                pos = i * ColorOrder.BaseOrderLength_Normal
                lst.extend(self.__order[ pos + 4 : pos + 12])
        return lst
    
    def mix(self, co, mixtype = 'Connect'):
        mixtype = mixtype.capitalize()
        if mixtype == 'Connect':
            self.__order.extend(co.__order)
        elif mixtype == 'Cross':
            lst = []
            idx1 = 0
            idx2 = 0
            for i in range(ColorOrder.BaseOrderLength_Normal):
                for j in range(self.__baseOrderNumber):
                    lst.append(self.__order[idx1])
                    idx1 += 1
                for j in range(co.__baseOrderNumber):
                    lst.append(co.__order[idx2])
                    idx2 += 1
            self.__order = lst
        self.__length += co.__length
        self.__baseOrderNumber += co.__baseOrderNumber

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

其实是补之前没交的sql作业

1.非常基本的操作

新建数据库

​

1

create database L4C2

新建表

PID为主键

​

1
2
3
4
5
6
7
8
9

create table L4C2.dbo.Person
(
	PID nchar(15),
	PName nchar(25),
	PRole nchar(10),
	Lucky int,
	Ammo int
	primary key(PID)
)

增加列

​

1

alter table L4C2.dbo.Person add Ping int

修改列

修改列的数据类型

​

1

alter table L4C2.dbo.Person alter column Lucky varchar(10)

删除列

​

1

alter table L4C2.dbo.Person drop column Lucky

给表增加行

增加多行，给所有列赋值

​

1
2
3
4
5
6

insert into L4C2.dbo.Person values
(1234567,'EVO.T im a','Ellis',700,230),
(1234568,'EVO.Star','Smoker',0,225),
(1234569,'Double.Mayuyu','Coach',80,40),
(1234570,'dec.nv','Nick',0,233),
(1234571,'kain.nv','Charger',0,125);

给特定列赋值

​

1

insert into L4C2.dbo.Person (PID,PName,PRole) values (7654321,'NPC.Bilibili.Deadz','spectator')

创建索引

按照Ping创建降序索引

​

1

create index idx_Ping on L4C2.dbo.Person(Ping desc)

按照Ammo创建升序索引

​

1

create index idx_Ammo on L4C2.dbo.Person(Ping asc)

删除索引

​

1

drop index idx_Ping on L4C2.dbo.Person

2.查询训练

1.查找年级为2001的学生，按学号降序排列

​

1
2
3

select STname from University.dbo.Student
where STgrade = 2001
order by STid desc

查找年级为2001的学生，按学号升序排列

​

1
2
3

select STname from University.dbo.Student
where STgrade = 2001
order by STid asc

查询所有选课课程中及格的分数，并将其换算为绩点（60分为1，每增加一分，绩点+0.1）

​

1
2

select (SCore-60)/10+1 from University.dbo.SC
where SCore >= 60

查询课时为48或24的课程的名称

​

1
2

select CRname from University.dbo.Course x
where x.CRtimes=48 or x.CRtimes=24

查询课程名中带有data的课程的编号

​

1
2

select CRid from University.dbo.Course x
where x.CRname like '%data%'

查询所有选课记录中的课程号，不重复显示

​

1

select distinct CRid from University.dbo.SC x

老师的平均工资

​

1

select avg(THsalary) from University.dbo.Teacher

查询所有学生编号和平均成绩，按照平均成绩降序排序

​

1
2
3

select STid,avg(SCore) from University.dbo.SC
group by STid
order by avg(SCore) desc

统计所有课程的选课人数和平均成绩

​

1
2
3

select CRid,count(CRid) '人数',avg(SCore) '平均成绩'
from University.dbo.SC
group by CRid

查询至少选修了三门课的学生号

​

1
2
3

select STid from University.dbo.SC
group by STid
having count(*) >= 3

查询学号为2001001的学生选修的课程名和成绩

​

1
2
3

select CRname,Score 
from University.dbo.SC s, University.dbo.Course c
where s.CRid = c.CRid and s.STid = '2001001'

查询所有选了database课的学生id

​

1
2
3

select STid
from University.dbo.Course c , University.dbo.SC sc
where c.CRname = 'database' and sc.CRid = c.CRid

查询所有选了同一课程的学生对

​

1
2
3

select distinct x.STid A,y.STid B
from University.dbo.SC x,University.dbo.SC y
where x.CRid = y.CRid and x.STid<y.STid

查询至少有两人选修的课程id

​

1
2
3
4

select CRid
from University.dbo.SC
group by CRid
having count(*) >=2

查询跟学号2001001的学生共同上课的学生的编号

​

1
2
3

select distinct y.STid
from University.dbo.SC x, University.dbo.SC y
where x.CRid = y.CRid and x.STid = '2001001'and x.STid <> y.STid

查询学号为2001001的学生的姓名，以及其所有选课的课程名与成绩

​

1
2
3

select distinct s.STname,c.CRname,sc.SCore
from University.dbo.SC sc , University.dbo.Course c , University.dbo.Student s
where s.STid = sc.STid and sc.CRid = c.CRid and s.STid = '2001001'

查询所有选了课的学生的基本信息以及课程名和成绩

​

1
2
3

select distinct s.STid,s.STname,s.STgrade,c.CRname,sc.SCore
from University.dbo.SC sc , University.dbo.Course c , University.dbo.Student s
where s.STid = sc.STid and sc.CRid = c.CRid

查询与学号为2001001同年级的学生的信息

​

1
2
3
4
5
6
7

select *
from University.dbo.Student
where STgrade = (
	select STgrade
	from University.dbo.Student
	where STid = '2001001'
)

​

查询所有选了课的学生信息

​

1
2
3
4
5
6

select *
from University.dbo.Student
where STid in (
	select STid
	from University.dbo.SC
)

​

查询没有人选的课程的编号

​

1
2
3
4
5
6

select CRid
from University.dbo.Course
where CRid not in (
	select CRid
	from University.dbo.SC
)

查询所有选了课程名为cpp的课程的学生姓名

​

1
2
3
4
5
6
7
8
9
10
11

select STname
from University.dbo.Student
where STid in (
	select STid
	from University.dbo.SC
	where CRid in(
		select CRid
		from University.dbo.Course
		where CRname = 'cpp'
	)
)

​

查询成绩最差的成绩状况

​

1
2
3
4

select * from University.dbo.SC x
where x.SCore <= ALL(
	select SCore from SC where SCore is not NULL
)

查询课时跟python或java一样长的课程名

​

1
2
3
4
5

select CRname from University.dbo.Course
where CRtimes = some(
select CRtimes from University.dbo.Course x
where CRname = 'Java' or CRname = 'Python'
)

查询选了1001号课的学生名字

​

1
2
3
4
5

select STname from University.dbo.Student y
where exists(
	select * from University.dbo.SC x
	where x.CRid = '1001' and y.STid = x.STid
)

查询选修了所有课程的学生的姓名

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

洛谷 P1048采药

https://www.luogu.com.cn/problem/P1048

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <queue>
#include <map>
#include <set>
#include <stack>
#include <vector>
typedef long long LL;
typedef std::pair<int ,int> PP;
const int N = 105;
int tm[N],va[N],dp[1005];
int tt,m;

int main()
{
   std::cin >> tt >> m;
   memset(dp,0,sizeof(dp));
   for(int i=1; i<=m; i++) std::cin >> tm[i] >> va[i];
   for(int i=1; i<=m; i++){
      for(int j=tt; j>=tm[i]; j--){
         dp[j] = std::max(dp[j],dp[j-tm[i]]+va[i]);
      }
   }
   std::cout << dp[tt];
   return 0;
}

​
​

洛谷 P1060 开心的金明

https://www.luogu.com.cn/problem/P1060

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <queue>
#include <map>
#include <set>
#include <stack>
#include <vector>
typedef long long LL;
typedef std::pair<int ,int> PP;
const int N = 105,M = 30005;
int va[N],we[N],dp[M];
int tt,m;

int main()
{
   std::cin >> tt >> m;
   for(int i=0; i<m; i++){
      std::cin >> va[i] >> we[i];
   }
   for(int i=0; i<m; i++){
      for(int j=tt; j>=va[i]; j--){
         dp[j] = std::max(dp[j], dp[j-va[i]]+va[i]*we[i]);
      }
   }
   std::cout << dp[tt];
   return 0;
}

​

洛谷 P1855 榨取kkksc03

https://www.luogu.com.cn/problem/P1855
有两样限制的01背包，思路不变

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <queue>
#include <map>
#include <set>
#include <stack>
#include <vector>
typedef long long LL;
typedef std::pair<int ,int> PP;
const int N = 205,M = 105;
int dp[N][N];
int mo[M],tm[M];
int n,m,t;
int main()
{
   scanf("%d%d%d",&n,&m,&t);
   for(int i=0; i<n; i++){
      scanf("%d%d",&mo[i],&tm[i]);
   }
   for(int i=0; i<n; i++){
      for(int j=m; j>=mo[i]; j--){
         for(int k=t; k>=tm[i]; k--){
            dp[j][k] = std::max(dp[j][k],dp[j-mo[i]][k-tm[i]]+1);
         }
      }
   }
   printf("%d",dp[m][t]);
   return 0;
}

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

题目描述

Word puzzles are usually simple and very entertaining for all ages. They are
so entertaining that Pizza-Hut company started using table covers with word
puzzles printed on them, possibly with the intent to minimise their client’s
perception of any possible delay in bringing them their order.

Even though word puzzles may be entertaining to solve by hand, they may become
boring when they get very large. Computers do not yet get bored in solving
tasks, therefore we thought you could devise a program to speedup (hopefully!)
solution finding in such puzzles.

The following figure illustrates the PizzaHut puzzle. The names of the pizzas
to be found in the puzzle are: MARGARITA, ALEMA, BARBECUE, TROPICAL, SUPREMA,
LOUISIANA, CHEESEHAM, EUROPA, HAVAIANA,
CAMPONESA.![在这里插入图片描述](https://imgconvert.csdnimg.cn/aHR0cHM6Ly92ai56MTgwLmNuL2QwYzAxMDE5MTcwNDBkMTY2NTgzYmE5YzNhYWQ4Yzkz?x-oss-
process=image/format,png)
Your task is to produce a program that given the word puzzle and words to be
found in the puzzle, determines, for each word, the position of the first
letter and its orientation in the puzzle.

You can assume that the left upper corner of the puzzle is the origin, (0,0).
Furthemore, the orientation of the word is marked clockwise starting with
letter A for north (note: there are 8 possible directions in total).

输入

The first line of input consists of three positive numbers, the number of
lines, 0 < L <= 1000, the number of columns, 0 < C <= 1000, and the number of
words to be found, 0 < W <= 1000. The following L input lines, each one of
size C characters, contain the word puzzle. Then at last the W words are input
one per line.

输出

Your program should output, for each word (using the same order as the words
were input) a triplet defining the coordinates, line and column, where the
first letter of the word appears, followed by a letter indicating the
orientation of the word according to the rules define above. Each value in the
triplet must be separated by one space only.

输入样例

20 20 10
QWSPILAATIRAGRAMYKEI
AGTRCLQAXLPOIJLFVBUQ
TQTKAZXVMRWALEMAPKCW
LIEACNKAZXKPOTPIZCEO
FGKLSTCBTROPICALBLBC
JEWHJEEWSMLPOEKORORA
LUPQWRNJOAAGJKMUSJAE
KRQEIOLOAOQPRTVILCBZ
QOPUCAJSPPOUTMTSLPSF
LPOUYTRFGMMLKIUISXSW
WAHCPOIYTGAKLMNAHBVA
EIAKHPLBGSMCLOGNGJML
LDTIKENVCSWQAZUAOEAL
HOPLPGEJKMNUTIIORMNC
LOIUFTGSQACAXMOPBEIO
QOASDHOPEPNBUYUYOBXB
IONIAELOJHSWASMOUTRK
HPOIYTJPLNAQWDRIBITG
LPOINUYMRTEMPTMLMNBO
PAFCOPLHAVAIANALBPFS
MARGARITA
ALEMA
BARBECUE
TROPICAL
SUPREMA
LOUISIANA
CHEESEHAM
EUROPA
HAVAIANA
CAMPONESA

输出样例

0 15 G
2 11 C
7 18 A
4 8 C
16 13 B
4 15 E
10 3 D
5 1 E
19 7 C
11 11 H

瞎翻译

给你一张字谜图，里头有一堆乱七八糟的字母，
输入：
先输入仨数L,C,W，前两个(L,C)是字谜图的行数和列数，第三个(W)是输入单词的数目，
之后输入L行C列的数填满字谜图，
最后W行输入W个字符串，这W个字符串肯定都可以在字谜图上找到（字母横着竖着或斜着线性连续）
输出：
一行输出三个元素，前两个是找到的字符串的首字母的坐标，第三个是字符串的排列方向（从首字母到尾字母的方向），方向一共有8个，按照顺时针旋转，A代表正上方，B代表右上方，一次类推

使用trie树暴力破解

思路： 用所有所查询的字符串建立一颗trie树，然后遍历地图上的每个点，在每个点分别朝8个方向对trie树搜索（三重循环无脑搜就完了）

​

1
2
3
4
5
6
7
8
9
10
11
12
13

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

const int dy[8]={0,1,1,1,0,-1,-1,-1};//设左上角为原点，向下为x轴正方向，向右为y轴正方向
const int dx[8]={-1,-1,0,1,1,1,0,-1};//先设置好移动方向，dx[0],dy[0]为向上方向（A方向），方向按照顺时针旋转顺序写
const int maxn=1005;
char cell[maxn][maxn],word[maxn];//cell储存字谜地图，word用于接收一个要搜索的单词
int slen[maxn],tidx,r,c,w,ans[maxn][3];//slen储存每个要搜索的单词的长度，tidx为节点序号，ans储存答案（方向+横纵坐标）
struct Node{
    int id,next[26];//在trie树中每个单词的结尾给id赋值，其值为 这个单词按照输入顺序排的序号（从1开始，不是0）
}treeN[maxn*maxn];

​

1
2
3
4
5
6
7
8
9
10
11
12
13

//每输入一个单词，进行一次此函数，把单词存入trie树
void joinTree(int id)
{
    int root=0,len=strlen(word),nxt;
    slen[id]=len;       //把此字符串的长度储存在len数组中
    for(int i=0; i<len; i++){
        nxt=word[i]-'A';
        if(treeN[root].next[nxt]<=0)
            treeN[root].next[nxt]=++tidx;
        root=treeN[root].next[nxt];
    }
    treeN[root].id=id;//在trie树中每个单词的结尾给id赋值，其值为 这个单词按照输入顺序排的序号（从1开始，不是0）
}

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

//查找函数
void sch(int x,int y,int dir){
    int root=0,id;
    while(x>=0 && x<=r && y>=0 && y<=c){    //在不越界的条件下不断沿trie树搜索
        root=treeN[root].next[cell[x][y]-'A'];
        if(root<=0) break;
        id=treeN[root].id;
        if(id>0){   //若id>0，说明这个位置是第id个单词的结尾，略微处理得到答案，存入ans数组
            ans[id][0]=dir;
            ans[id][1]=x-(slen[id]-1)*dx[dir];
            ans[id][2]=y-(slen[id]-1)*dy[dir];
        }
        x+=dx[dir];
        y+=dy[dir];
    }
}

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int main(){
    tidx=0;
    std::cin >> r >> c >> w;
    for(int i=0; i<r; i++)
        std::cin >> cell[i];
    for(int i=1; i<=w; i++){
        std::cin >> word;
        joinTree(i);
    }
    for(int i=0; i<r; i++)// 输入所有数据并建立好tire树后暴搜得到答案
        for(int j=0; j<c; j++)
            for(int k=0; k<8; k++)
                sch(i,j,k);
    for(int i=1; i<=w; i++)
        printf("%d %d %c\n",ans[i][1],ans[i][2],ans[i][0]+'A');
    return 0;
}

​

AC自动机解法

在trie树的基础上使用AC自动机（只需要多一步添加fail指针，然后再修改亿点点）
AC自动机的好处是只需要在地图最外围的一圈把8个方向都遍历一次就行了，因为它不用像单纯用trie树一样每次只能从根节点开始搜索，而是匹配不成功时通过fail指针转移到树的其他位置继续搜索

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
//相对于暴搜，用AC自动机在地图最外围的一圈把8个方向都遍历一次

const int dy[8]={0,1,1,1,0,-1,-1,-1};
const int dx[8]={-1,-1,0,1,1,1,0,-1};
const int maxn=1005;
char cell[maxn][maxn],word[maxn];
int slen[maxn],tidx,r,c,w,ans[maxn][3];
struct Node{
    int id,next[26],fail;
}treeN[maxn*maxn];
void joinTree(int id)
{
    int root=0,len=strlen(word),nxt;
    slen[id]=len;
    for(int i=0; i<len; i++){
        nxt=word[i]-'A';
        if(treeN[root].next[nxt]<=0)
            treeN[root].next[nxt]=++tidx;
        root=treeN[root].next[nxt];
    }
    treeN[root].id=id;
}

//建立好trie树后调用此函数通过bfs添加fail指针
void getFail()
{
    int nxt,cur,fail;
    std::queue<int> q;
    for(int i=0; i<26; i++){
        nxt=treeN[0].next[i];
        if(nxt>0){
            treeN[nxt].fail=0;
            q.push(nxt);
        }
    }
    while(!q.empty()){
        cur=q.front(),q.pop();
        fail=treeN[cur].fail;
        for(int i=0; i<26; i++){
            nxt=treeN[cur].next[i];
            if(nxt>0){
                treeN[nxt].fail=treeN[fail].next[i];
                q.push(nxt);
            }
            else treeN[cur].next[i]=treeN[fail].next[i];
        }
    }
}

void ACgo(int x,int y,int dir){
    int root=0,id;
    while(x>=0 && x<=r && y>=0 && y<=c){
        while( root>0 && treeN[root].next[cell[x][y]-'A']<=0)//如果不能匹配就通过fail指针回溯，在trie的其他位置继续寻找，节约了时间
            root=treeN[root].fail;
        root=treeN[root].next[cell[x][y]-'A'];
        id=treeN[root].id;
        if(id>0){
            ans[id][0]=dir;
            ans[id][1]=x-(slen[id]-1)*dx[dir];
            ans[id][2]=y-(slen[id]-1)*dy[dir];
        }
        x+=dx[dir];
        y+=dy[dir];
    }
}
int main(){
    tidx=0;
    std::cin >> r >> c >> w;
    for(int i=0; i<r; i++)
        std::cin >> cell[i];
    for(int i=1; i<=w; i++){
        std::cin >> word;
        joinTree(i);
    }
    getFail();
    for(int i=0; i<r; i++)
        for(int j=0; j<8; j++)
            ACgo(i,0,j),ACgo(i,r-1,j);
    for(int i=0; i<c; i++)
        for(int j=0; j<8; j++)
            ACgo(0,i,j),ACgo(c-1,i,j);
    for(int i=1; i<=w; i++)
        printf("%d %d %c\n",ans[i][1],ans[i][2],ans[i][0]+'A');
    return 0;
}

​

反向构建trie树，不用记录单词长度

两段代码都只改了一点，但都时间超限，目前没发现原因，慎看
两段代码都只改了一点，但都时间超限，目前没发现原因，慎看
两段代码都只改了一点，但都时间超限，目前没发现原因，慎看
两段代码都只改了一点，但都时间超限，目前没发现原因，慎看
两段代码都只改了一点，但都时间超限，目前没发现原因，慎看

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
const int dy[8]={0,-1,-1,-1,0,1,1,1};
const int dx[8]={1,1,0,-1,-1,-1,0,1};
const int maxn=1005;
char cell[maxn][maxn],word[maxn];
int tidx,r,c,w,ans[maxn][3];
struct Node{
    int id,next[26],fail;
}treeN[maxn*maxn];
void joinTree(int id)
{
    int root=0,len=strlen(word),nxt;
    for(int i=len-1; i>=0; i--){
        nxt=word[i]-'A';
        if(treeN[root].next[nxt]<=0)
            treeN[root].next[nxt]=++tidx;
        root=treeN[root].next[nxt];
    }
    treeN[root].id=id;
}
void getFail()
{
    int nxt,cur,fail;
    std::queue<int> q;
    for(int i=0; i<26; i++){
        nxt=treeN[0].next[i];
        if(nxt>0){
            treeN[nxt].fail=0;
            q.push(nxt);
        }
    }
    while(!q.empty()){
        cur=q.front(),q.pop();
        fail=treeN[cur].fail;
        for(int i=0; i<26; i++){
            nxt=treeN[cur].next[i];
            if(nxt>0){
                treeN[nxt].fail=treeN[fail].next[i];
                q.push(nxt);
            }
            else treeN[cur].next[i]=treeN[fail].next[i];
        }
    }
}
void ACgo(int x,int y,int dir){
    int root=0,id;
    while(x>=0 && x<=r && y>=0 && y<=c){
        while( root>0 && treeN[root].next[cell[x][y]-'A']<=0)
            root=treeN[root].fail;
        root=treeN[root].next[cell[x][y]-'A'];
        id=treeN[root].id;
        if(id>0){
            ans[id][0]=dir;
            ans[id][1]=x;
            ans[id][2]=y;
        }
        x+=dx[dir];
        y+=dy[dir];
    }
}
int main(){
    tidx=0;
    std::cin >> r >> c >> w;
    for(int i=0; i<r; i++)
        std::cin >> cell[i];
    for(int i=1; i<=w; i++){
        std::cin >> word;
        joinTree(i);
    }
    getFail();
    for(int i=0; i<r; i++)
        for(int j=0; j<8; j++)
            ACgo(i,0,j),ACgo(i,r-1,j);
    for(int i=0; i<c; i++)
        for(int j=0; j<8; j++)
            ACgo(0,i,j),ACgo(c-1,i,j);
    for(int i=1; i<=w; i++)
        printf("%d %d %c\n",ans[i][1],ans[i][2],ans[i][0]+'A');
    return 0;
}

​
​
​
​

1
2
3
4
5
6
7
8
9
10
11
12
13

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>

const int dy[8]={0,-1,-1,-1,0,1,1,1};//设左上角为原点，向下为x轴正方向，向右为y轴正方向
const int dx[8]={1,1,0,-1,-1,-1,0,1};//先设置好移动方向，dx[0],dy[0]为向上方向（A方向），方向按照顺时针旋转顺序写
const int maxn=1005;
char cell[maxn][maxn],word[maxn];//cell储存字谜地图，word用于接收一个要搜索的单词
int tidx,r,c,w,ans[maxn][3];//tidx为节点序号，ans储存答案（方向+横纵坐标）
struct Node{
    int id,next[26];//在trie树中每个单词的结尾给id赋值，其值为 这个单词按照输入顺序排的序号（从1开始，不是0）
}treeN[maxn*maxn];

​

1
2
3
4
5
6
7
8
9
10
11
12

//每输入一个单词，进行一次此函数，把单词存入trie树
void joinTree(int id)
{
    int root=0,len=strlen(word),nxt;
    for(int i=len-1; i>=0; i--){
        nxt=word[i]-'A';
        if(treeN[root].next[nxt]<=0)
            treeN[root].next[nxt]=++tidx;
        root=treeN[root].next[nxt];
    }
    treeN[root].id=id;//在trie树中每个单词的结尾给id赋值，其值为 这个单词按照输入顺序排的序号（从1开始，不是0）
}

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

//查找函数
void sch(int x,int y,int dir){
    int root=0,id;
    while(x>=0 && x<=r && y>=0 && y<=c){    //在不越界的条件下不断沿trie树搜索
        root=treeN[root].next[cell[x][y]-'A'];
        if(root<=0) break;
        id=treeN[root].id;
        if(id>0){   //若id>0，说明这个位置是第id个单词的结尾，略微处理得到答案，存入ans数组
            ans[id][0]=dir;
            ans[id][1]=x;
            ans[id][2]=y;
        }
        x+=dx[dir];
        y+=dy[dir];
    }
}

​

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int main(){
    tidx=0;
    std::cin >> r >> c >> w;
    for(int i=0; i<r; i++)
        std::cin >> cell[i];
    for(int i=1; i<=w; i++){
        std::cin >> word;
        joinTree(i);
    }
    for(int i=0; i<r; i++)// 输入所有数据并建立好tire树后暴搜得到答案
        for(int j=0; j<c; j++)
            for(int k=0; k<8; k++)
                sch(i,j,k);
    for(int i=1; i<=w; i++)
        printf("%d %d %c\n",ans[i][1],ans[i][2],ans[i][0]+'A');
    return 0;
}

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

https://vjudge.net/contest/389071#problem/B

题目描述

On a grid map there are n little men and n houses. In each unit time, every
little man can move one unit step, either horizontally, or vertically, to an
adjacent point. For each little man, you need to pay a $1 travel fee for every
step he moves, until he enters a house. The task is complicated with the
restriction that each house can accommodate only one little man.

Your task is to compute the minimum amount of money you need to pay in order
to send these n little men into those n different houses. The input is a map
of the scenario, a ‘.’ means an empty space, an ‘H’ represents a house on that
point, and am ‘m’ indicates there is a little man on that point.

![在这里插入图片描述](https://imgconvert.csdnimg.cn/aHR0cHM6Ly92ai56MTgwLmNuLzI5ZGE0YzIyY2Q5YTM1ZWI5NmIyYTA4Yjc1Y2U4NDIw?x-oss-
process=image/format,png#pic_center)

You can think of each point on the grid map as a quite large square, so it can
hold n little men at the same time; also, it is okay if a little man steps on
a grid with a house without entering that house.

输入

There are one or more test cases in the input. Each case starts with a line
giving two integers N and M, where N is the number of rows of the map, and M
is the number of columns. The rest of the input will be N lines describing the
map. You may assume both N and M are between 2 and 100, inclusive. There will
be the same number of 'H’s and 'm’s on the map; and there will be at most 100
houses. Input will terminate with 0 0 for N and M.

输出

For each test case, output one line with the single integer, which is the
minimum amount, in dollars, you need to pay.

样例输入

2 2
.m
H.
5 5
HH…m
…
…
…
mm…H
7 8
…H…
…H…
…H…
mmmHmmmm
…H…
…H…
…H…
0 0

样例输出

2
10
28

瞎翻译

给你一张地图，地图被分割成了N行M列的网格。

第一行：输入N，M表示地图大小。

第2 到 第N+1行： 输入地图内容， .代表空地，m代表人，H代表房子。

N和M不大于100，房子数目不大于100

人和房子的数量是相等的，而人要移动进入房子，且每个房子只能进一个人。
不过人每移动一格（横移或者竖移）要花一块钱。

问：
要使人都进入房子最少花多少钱？
（地图的每一格都足够大，可以容纳无限多的人。）

题解

思路：
1.
地图最大为100x100 ，所以人最多花不到200元钱，我们定一个常数ML=210.
2.
先计算每个人到每个房子需要花的钱，用ML减去需要花的钱，得到的数值，存进数组map[][]（不是地图，我取的映射的意思）

这么存的原因是：KM算法可以算出最多要花多少钱，然而我们需要求最少要花多少钱，这样就只需要把“最小的”先暂时变成“最大的”，完成KM算法之后再额外通过一步计算得到正确答案。

推导可知：正确答案=（ML*房子数量）-KM算法得到的最大值

​
​ #include
​ #include
​ #include
​ #include
​
const int maxn=110;
const int ML=220;//花费不可能超过200
char cell[maxn][maxn];
int map[maxn][maxn],lx[maxn],ly[maxn],link[maxn];
//map取的意思是映射，map[i][j]表示第i个人到第j个房子的距离
//lx表示人顶标的值，ly表示房子顶标的值
bool visx[maxn],visy[maxn];
int pnum,ans;
struct Node
{
int x,y;
}person[maxn],house[maxn];

bool dfs(int x)
{

    visx[x]=true;
    for(int i=0; i<pnum ;i++)
    {
//这里的lx[x]一开始写成了lx[i]，找bug找了半天，巨麻烦，打标记警醒一下
        if(!visy[i] && lx[x]+ly[i]==map[x][i])
        {
            visy[i]=true;
            if(link[i]==-1 || dfs(link[i]))
            {
                link[i]=x;
                return true;
            }
        }
    }
    return false;
}

int km()
{
    memset(lx,0,sizeof(lx));
    memset(ly,0,sizeof(ly));
    memset(link,-1,sizeof(link));
    for(int i=0; i<pnum ; i++)
        for(int j=0; j<pnum; j++)
        {
            lx[i]=std::max(lx[i],map[i][j]);
        }
    for(int i=0; i<pnum; i++)
    {
        memset(visx,false,sizeof(visx));
        memset(visy,false,sizeof(visy));
        while(!dfs(i))
        {
            int tmp=ML;

//--------------------------->>特此标记<<-----------------------------
// KM没学好，这里一开始想错了，误认为下面tmp=min（）式子中lx的下标一定是i，
//导致下方两行没要，一直错被卡了很长时间

            for(int j=0; j<pnum; j++)
                if(visx[j])
//*******************************************************************************
                    for(int k=0; k<pnum; k++)
                        if(visy[k]==false)
                            tmp=std::min(tmp,lx[j]+ly[k]-map[j][k]);
            for(int j=0; j<pnum; j++)
            {
                if(visx[j])
                    lx[j]-=tmp;
                if(visy[j])
                    ly[j]+=tmp;
            }
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));
        }
    }
    ans=0;
    for(int i=0;i<pnum; i++)
    {
        ans+=lx[i]+ly[i];
    }
    return ML*pnum-ans;
}

int main()
{
    int n,m;
    int p,h;
    while(std::cin >> n >> m && !(n==0 && m==0))
    {
        p=h=0;
        for(int i=0;i <n; i++)
            for(int j=0; j<m ; j++)
            {
                std::cin >> cell[i][j];
                if(cell[i][j]=='m')
                {
                    person[p].x=i;
                    person[p++].y=j;
                }
                else if(cell[i][j]=='H')
                {
                    house[h].x=i;
                    house[h++].y=j;
                }
            }
        pnum=p;
        for(int i=0; i<p; i++)
            for(int j=0; j<h; j++)
            {
                map[i][j]=abs(person[i].x-house[j].x)+abs(person[i].y-house[j].y);
                map[i][j]=ML-map[i][j];
            }
        std::cout << km() << std::endl;
    }

    return 0;
}

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

1 线形石子合并

参考题目 https://www.acwing.com/problem/content/284/

题目要求最小代价

大致思路为：
有n组石头排成一条线，
规定把第i组和第i组合并（自己合并自己），代价为0
1.求所有相邻的两堆石头合并的代价
2.求所有相邻的三堆石头合并的代价，之前求出的两堆石头合并的代价可以作为前提
3.求所有相邻的四堆石头合并的代价，之前求出的两堆石头合并的代价和三堆石头合并的代价都可以作为前提
…
n-1.求相邻的n堆石头合并的代价，之前求出的【2，n-1】堆石头合并的代价都可以作为前提

用程序模拟出这个过程便可以求得答案
.

.

使用二维数组dp记录这些代价，首先令所有的dp[i][i]=0
使用一维数组sum记录从第一堆石头到第i堆石头的石头总数
假设要求解dp[4][7] 只需要求
sum[7]-sum[4-1] + min(dp[4] [4]+dp[5] [7],dp[4] [5]+dp[6] [7],dp[4] [6]+dp[7] [7])

代码:

​
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include

​

2 环形石子合并

这个知识点是我根据上方线形石子合并自己想的,大概有更优的解法吧

参考题目 https://www.luogu.com.cn/problem/P1880

把环形拆成线形 把环形的n堆石头从第1堆石头和第n堆石头之间分开,成为线形,然后再把这n堆在一条线上的石头复制一份,加到第n堆石头末尾.
这样即可模拟以 每 一堆石头为起点的 线形 石子合并

线形石子合并中for(int st=1; st+span<=n; st++)的st+span<=n是为了把ed限制在ed<=n,现在可以改成st<=n
其他地方基本与线形合并相同

需要注意dp数组的行数没有变成两倍,for(int tmp=st; tmp<ed; tmp++)中如果出现tmp+1>n
若要获取dp[tmp+1][ed]的值,则获取tmp[tmp+1-n][ed-n]的值

代码:

​
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include

​

说明 - 2022-05-05

本篇博客为本人原创, 原发布于CSDN, 在搭建个人博客后使用爬虫批量爬取并挂到个人博客, 出于一些技术原因博客未能完全还原到初始版本(而且我懒得修改), 在观看体验上会有一些瑕疵 ,若有需求会发布重制版总结性新博客。发布时间统一定为1111年11月11日。钦此。

倍增 构造O(nlogn)，在线(单次)查询O(logn)
tarjin 构造O(n) ，离线(全部)查询O(N+M)
根据题目 洛谷P3379【模板】最近公共祖先 的样例测试，tarjin和倍增不能通过占用的时间或空间评判高下，谁占优势应该跟数据的特征有关。

洛谷P3379【模板】最近公共祖先

倍增方法

构造fa数组的正确写法是这样的
for(int i=1; i<=20; i++){
fa[x][i] = fa[fa[x][i-1]][i-1];
}
然而第一遍错写成了这样
for(int i=1; i<=20; i++){
fa[x][i] = fa[father][i-1];
}
这显然是错误的，不是方法他的父亲的上2^{i-1个节点，而是访问它的上2}i-1个节点的上2^i-1个节点
引以为戒

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <map>
#include <stack>
#include <string>
#include <cstring>
#include <vector>
#include <cmath>
#include <set>
typedef long long int LL;
const int N = 5e5+5;
int fa[N][22],depth[N],head[N];
int n,m,s,u,v;
int idx;
struct Edge
{
    int to,nxt;
}edg[N<<1];
void addEdge(int fr,int to)
{
    edg[idx].to = to;
    edg[idx].nxt = head[fr];
    head[fr] = idx++;
}
void build(int x,int father)
{
    fa[x][0] = father;
    depth[x] = depth[father]+1;
    for(int i=1; i<=20; i++){
        fa[x][i] = fa[fa[x][i-1]][i-1];
    }
    for(int e=head[x]; e; e=edg[e].nxt){
        int y = edg[e].to;
        if(y!=father) build(y,x);
    }
}
int lca(int x,int y)
{
    if(depth[x] < depth[y]) std::swap(x,y);
    for(int i=20; i>=0; i--){
        if(fa[x][i]) if(depth[fa[x][i]]>=depth[y]){
            x = fa[x][i];
            if(depth[x] == depth[y]) break;
        }
    }
    if(x == y) return x;
    for(int i=20; i>=0; i--){
        if(fa[x][i]) if(fa[x][i] != fa[y][i]){
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[y][0];
}
int main()
{
    //freopen("D:\\EdgeDownloadPlace\\P3379_2.in","r",stdin);
    idx = 2;
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1; i<n; i++){
        scanf("%d%d",&u,&v);
        addEdge(u,v); addEdge(v,u);
    }
    build(s,0);
    for(int i=0; i<m; i++){
        scanf("%d%d",&u,&v);
        printf("%d\n",lca(u,v));
    }
    return 0;
}

倍增方法可以提前算log优化

​
​ #include
​ #include
​ #include
​ #include
​ #include

​

tarjin方法

​
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include

洛谷 P1967 [NOIP2013 提高组] 货车运输

最大生成树 + 倍增lca找最短距离
注意应该先更新ans，再使当前点倍增跳跃，刚才是有一处写反了，没注意到，导致WA

​
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include

求log优化版

​
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include
​ #include